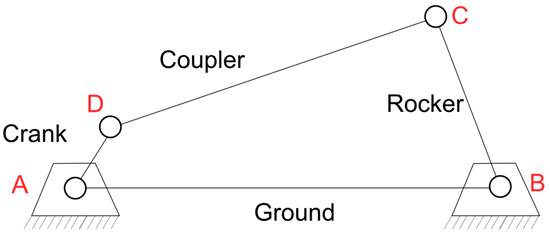
A four bar linkage or a four bar mechanism consists of the following four components:
- Crank
- Rocker
- Coupler
- Ground
Crank
Crank is a link which can rotate 360°. One of its end is fixed and the other moves around the first end. It only shows rotatory movement. The link AD is the rocker in figure shown above.
Rocker
Rocker is a link which shows to and from motion. It is not able to translate. One of its ends is also fixed. The link BC is the rocker in figure shown above.
Coupler
The link that connects rocker and crank is called coupler link. Both of its ends are able to move. So, it shows translator and rotatory movement. The link DC in the above figure is Coupler.
Ground
The ground link fixed from both ends. It does not move. It connects rocker and couple. The link AB in the above figure is ground link.
Lengths of links:
- Crank = 40 mm.
- Coupler = 180 mm.
- Rocker = 90 mm.
- Ground = 200 mm.
Grashof law
Grahsof law states that in a four bar linkage if the sum of lengths of shortest link and the longest link is equal to or less than the lengths of other two links, then the shortest link can rotate 360°.
So, if we write this in mathematical form:
S + L ≤ P + Q
- S = Shortest link = Crank
- L = Longest link = Ground
- P = Length of one intermediate link = Rocker
- Q = Length of other intermediate link. = Coupler
We get the following results when we apply the Grashof law to our links:
L + S = 200 + 40 = 240 mm P + Q = 90 + 180 = 270 mm
So, as we can see 240 < 270. The Grashof condition is satisfied.